1.
2.
Составляющие процесса передачи
информации
Передача информации происходит от источника к приемнику
информации.
Источником информации может быть все, что угодно: любой
объект или явление живой или неживой природы.
Процесс передачи информации протекает в материальной
среде, разделяющей источника и получателя информации,
которая называется каналом передачи информации.
Информация передается через канал в форме некоторой
последовательности сигналов, символов, знаков, которые
называются сообщением.
приемник информации — это объект, принимающий
сообщение, в результате чего происходят определенные
изменения его состояния.
3.
Клодом Шенноном была предложена модель процесса передачи
информации по техническим каналам связи, представленная схемой.
Под кодированием здесь понимается любое преобразование информации,
идущей от источника, в форму, пригодную для ее передачи по каналу связи.
Декодирование — обратное преобразование сигнальной последовательности.
4.
Пропускная способность канала
Разработчикам технических систем передачи информации приходится
решать две взаимосвязанные задачи:
1. как обеспечить наибольшую скорость передачи информации
2. как уменьшить потери информации при передаче.
Клод Шеннон был первым ученым, взявшимся за решение этих задач и
создавшим новую науку — теорию информации.
К.Шеннон определил способ измерения количества информации,
передаваемой по каналам связи.
пропускная способность канала — максимально возможная скорость
передачи информации.
Эта скорость измеряется в битах в секунду (а также килобитах в секунду,
мегабитах в секунду).
5.
Пропускная способность канала связи зависит от его технической
реализации. Например, в компьютерных сетях используются
следующие средства связи:
• телефонные линии (1-2 Мбит/с)
• электрическая кабельная связь
(Витая пара 10-100 Мбит/с, коаксиальный кабель до 10
Мбит/с)
• оптоволоконная кабельная связь (100-2000 Мбит/с)
• Радиосвязь (WiFi до 100 Мбит/с, Wimax до 70 Мбит/с)
6.
Шум
разного рода помехи, искажающие передаваемый сигнал и приводящие к потере
информации.
технические причины возникновения помех:
• плохое качество линий связи
• незащищенность друг от друга различных потоков информации,
передаваемых по одним и тем же каналам.
7.
Наличие шума приводит к потере передаваемой информации. В таких
случаях необходима защита от шума.
технические способы защиты каналов связи от воздействия шумов:
• использование экранированного кабеля вместо “голого” провода
• применение разного рода фильтров, отделяющих полезный сигнал от шума
Клодом Шенноном была разработана теория кодирования, дающая
методы борьбы с шумом.
.Основная идея Теории кодирования Шеннона
Передаваемый по линии связи код должен быть избыточным. За счет этого потеря какой-то
части информации при передаче может быть компенсирована.
Например, если при разговоре по телефону вас плохо слышно, то, повторяя каждое слово дважды, вы
имеете больше шансов на то, что собеседник поймет вас правильно
8.
Однако, нельзя делать избыточность слишком большой. Это приведет к
задержкам и удорожанию связи.
Теория кодирования позволяет получить такой код, который будет
оптимальным. При этом избыточность передаваемой информации
будет минимально возможной, а достоверность принятой
информации — максимальной.
В современных системах цифровой связи для борьбы с потерей
информации при передаче часто применяется метод пакетной
передачи данных:
Все сообщение разбивается на порции — пакеты. Для каждого пакета вычисляется контрольная
сумма (сумма двоичных цифр), которая передается вместе с данным пакетом. В месте приема
заново вычисляется контрольная сумма принятого пакета и, если она не совпадает с первоначальной
суммой, передача данного пакета повторяется. Так будет происходить до тех пор, пока исходная и
конечная контрольные суммы не совпадут.
9.
Классификация кодов
1. По основанию (количеству символов в алфавите):
бинарные (двоичные m=2) и не бинарные (m ? 2).
2. По длине кодовых комбинаций (слов):
равномерные — если все кодовые комбинации имеют одинаковую длину;
неравномерные — если длина кодовой комбинации не постоянна.
3. По способу передачи:
Последовательные, параллельные, блочные (данные сначала помещаются в
буфер, а потом передаются в канал) , бинарные непрерывные
4. По помехоустойчивости:
• простые (примитивные, полные) — для передачи информации используют все
возможные кодовые комбинации (без избыточности)
• корректирующие (помехозащищенные) — для передачи сообщений используют
не все, а только часть (разрешенных) кодовых комбинаций
10.
.
Классификация кодов
5. В зависимости от назначения и применения:
Внутренние коды — это коды, используемые внутри устройств
( машинные коды, а также коды, базирующиеся на использовании
позиционных систем счисления (двоичный, десятичный, двоичнодесятичный, восьмеричный, шестнадцатеричный и др.))
Коды для обмена данными и их передачи по каналам связи (ASCII,
EBCDIC)
Коды для специальных применений (код Грея, Коды Фибоначчи)
11.
.
ЦЕЛИ КОДИРОВАНИЯ
1) Повышение эффективности передачи данных,
за счет достижения максимальной скорости передачи данных.
2) Повышение помехоустойчивости при передаче данных.
1. Теория экономичного (эффективного, оптимального)
кодирования
занимается поиском кодов, позволяющих в каналах без помех
повысить эффективность передачи информации за счет устранения
избыточности источника и наилучшего согласования скорости
передачи данных с пропускной способностью канала связи.
2. Теория помехоустойчивого кодирования
занимается поиском кодов, повышающих достоверность передачи
информации в каналах с помехами.
12.
.
Решение задач
1. Согласно таблице windows-1251 (см тема 2.1.1) закодируйте
следующие слова: (кодирование, наследование, полиморфизм)
2. Согласно таблице windows-1251 (см тема 2.1.1) раскодируйте
следующие слова: (222 207 200 210 197 208, 199 197 204 203
223, 204 192 208 209)
Работа 1.4. Представление текстов. Сжатие текстов
Цель работы: практическое закрепление знаний о представлении в компьютере текстовых данных.
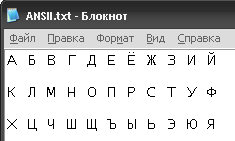
Задание 1
Определить, какие символы кодировочной таблицы ASCII (DOS) соответствуют всем прописным буквам русского алфавита в кодировочной таблице ANSI (Windows). Для выполнения задания создать текст с русским алфавитом в Блокноте, а затем открыть его в режиме просмотра (клавиша F3) в любом файловом менеджере (Windows Commander, Far, Total Commander, Norton Commander) и преобразовать в другую кодировку. После выполнения задания заполнить таблицу.
|
Буква в ANSI |
Буква в ASCII |
Буква в ANSI |
Буква в ASCII |
Буква в ANSI |
Буква в ASCII |
|
А |
К |
Х |
|||
|
Б |
Л |
Ц |
|||
|
В |
М |
Ч |
|||
|
Г |
Н |
Ш |
|||
|
Д |
О |
Щ |
|||
|
Е |
П |
Ъ |
|||
|
Ё |
Р |
Ы |
|||
|
Ж |
С |
Ь |
|||
|
З |
Т |
Э |
|||
|
И |
У |
Ю |
|||
|
Й |
Ф |
Я |
1. Используем готовый текстовый файл ANSI.txt..
2. Далее открывает Unreal Commander (Free Commander) и ищем в нём наш файл.
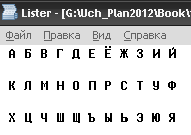
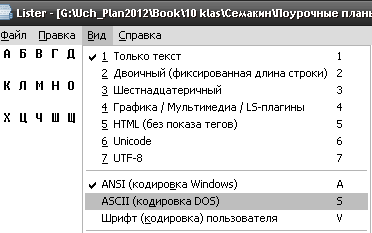
4. Затем нажимаем на режим просмотра F3. Там отобразится содержимое файла в изначальной кодировке (ANSI) и там же есть возможность, просмотреть это же содержимое в разных кодировках.
В нашем случае нужно найти значение кодировки ASCII (DOS).
5. Получаем результат:
Ответ: Таких символов нет. Вместо них на экране в режиме просмотра появляются символы псевдографики.
Задание 2
Закодировать текст с помощью кодировочной таблицы ASCII.
Happy Birthday to you!
Записать двоичное и шестиадцатеричное представления кода (для записи шестнадцатеричного кода использовать средство для просмотра файлов любого файлового менеджера).
в 16-ричной СС (используем кодовую таблицу в текстовом файле ASCII.docx)
48 61 70 70 79 20 42 69
72 74 68 64 61 79 20 74
6F 20 79 6F 75 21 21
в двоичной СС (4816=100 10002 где 1000 — код цифру 8, а 100 — код цифры 4)
1001000 1100001 1110000 1110000 1111001 0100000 1000010 1101001
1110010 1110100 1101000 1100100 1100001 1111001 0100000 1110100
1101111 0100000 1111001 1101111 1110101 0100001 0100001
Задание 3
Декодировать текст, записанный в международной кодировочной таблице ASCII (дано десятичное представление).
72 101 108 108 111 44 32 109 121 32 102 114 105 101 110 100 33
Для раскодирования используем таблицу в файле «Коды символов ASCII.mht»
где Dec — десятизначный код
Ответ: Hello, my friend!
Задание 4
Пользуясь таблицей кодировки ASCII, расшифровать текст, представленный в виде двоичных кодов символов.
01010000 01100101 01110010 01101110 00100000 01010101 01101110 01101001 01110110 01100101 01110010 01110011 01101001 01110100 01111001
Переведем в 16-ричный код отделяя группу двоичных разрядов, справа налево, по 4 бита:
01010000=0101 0000=5016
Используя кодовую таблицу из файла Коды символов ASCII.mht по найденному Hex коду (50) определим первый символ латинского текста «P»
50 65 72 6E 20 55 6D 69 76
65 72 73 69 74 79
Ответ: Perm University
Задание 5
Пользуясь кодовой страницей Windows-1251 таблицы кодировки ASCII, получить шестнадцатеричный код слова ИНФОРМАТИЗАЦИЯ.
Используем кодовую таблицу в файле «Таблица Windows-1251.mht»
Согласно этой таблицы русская заглавная буква «И» (в колонке Hex)
имеет 16-ричный код — C8
Ответ: C8 CD D4 CE D0 CC C0 D2 C8 C7 C0 D6 C8 DF
Задание 6
Во сколько раз увеличится объем памяти, необходимый для хранения текста, если его преобразовать из кодировки KOI8-R в кодировку Unicode?
Для кодирования одного символа в кодировке KOI-8 используется 1 байт, а в кодировке UNICODE — 2 байта, следовательно, информационный объем страницы текста увеличится в 2 раза
Ответ: в 2 раза
Задание 7
С помощью табличного процессора Excel построить кодировочную таблицу ASCII, в которой символы будут автоматически отображаться на экране в соответствии с их заданным десятичным номером (использовать соответствующую текстовую функцию).
Введите ускоренным методом числа от 33 до 254 (по 25 в каждой строке через столбец:
А, С, E, … , Q)
В ячейку B1 введите формулу =СИМВОЛ(A1) и далее используя ускоренный метод, скопируйте ее в остальные ячейки столбцов: B, D, F,…, R.
Справка:
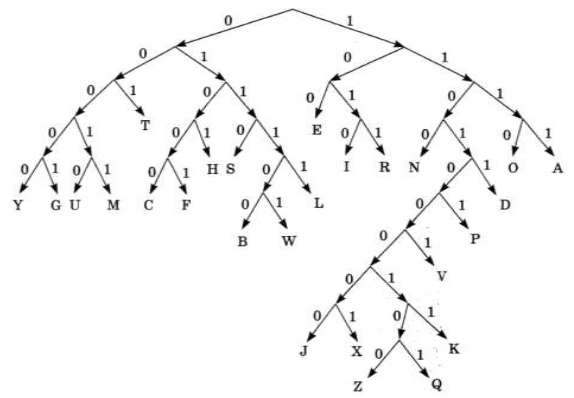
Алгоритм Хаффмана. Сжатием информации в памяти компьютера называют такое ее преобразование, которое ведет к сокращению объема занимаемой памяти при сохранении закодированного содержания. Рассмотрим один из способов сжатия текстовой информации — алгоритм Хаффмана. С помощью этого алгоритма строится двоичное дерево, которое позволяет однозначно декодировать двоичный код, состоящий из символьных кодов различной длины. Двоичным называется дерево, из каждой вершины которого выходят две ветви. На рисунке приведен пример такого дерева, построенного для алфавита английского языка с учетом частоты встречаемости его букв.
Закодируем с помощью данного дерева слово «hello»: 0101 100 01111 01111 1110
При размещении этого кода в памяти побитно он примет вид: 01011000 11110111 11110
Таким образом, текст, занимающий в кодировке ASCII 5 байтов, в кодировке Хаффмана займет только 3 байта.
Задание 8
Используя метод сжатия Хаффмана, закодируйте следующие слова:
а) administrator 1111 11011 00011 1010 1100 1010 0110 001 1011 1111 001 1110 1011
(11111101 10001110 10110010 10011000 11011111 10011110 1011)
б) revolution 1011 100 1101001 1110 01111 00010 001 1010 1110 1100
(10111001 10100111 10011110 00100011 01011101 100)
в) economy 100 01000 1110 1100 1110 00011 00000 (10001000 11101100 11100001 100000)
г) department 11011 100 110101 1111 1011 001 00011 100 1100 001
(11011100 11010111 11101100 10001110 01100001)
Задание 9
Используя дерево Хаффмана, декодируйте следующие слова:
а) 01110011 11001001 10010110 10010111 100000
(011100 1111 001 001 100 1011 01001 01111 00000) BATTERFLY
б) 00010110 01010110 10011001 01101101 01000100 000
(00010 1100 1010 1101001 100 1011 0110 1010 001 00000) UNIVERSITY
Информатика, 10 класс. Урок № 14.
Тема — Кодирование текстовой информации
Цели и задачи урока:
— познакомиться со способами кодирования и декодирования текстовой информации с помощью кодовых таблиц и компьютера;
— познакомиться со способом определения информационного объема текстового сообщения;
— познакомиться с алгоритмом Хаффмана.
Вся информация в компьютере хранится в двоичном коде. Поэтому надо научиться преобразовывать символы в двоичный код.
Формула Хартли определяет количество информации в зависимости от количества возможных вариантов:
N=2i, где
N — это количество вариантов,
i — это количество бит, не обходимых для кодирования.
Если же мы преобразуем эту формулу и примем за N — количество символов в используемом алфавите (назовем это мощностью алфавита), то мы поймем, сколько памяти потребуется для кодирования одного символа.
N=2i, где N — кол-во возможных вариантов
i — кол-во бит, потребуемых для кодирования
Итак, если в нашем алфавите будет присутствовать только 32 символа, то каждый из них займет только 5 бит.
И тогда каждому символу мы дадим уникальный двоичный код. Такую таблицу мы будем назвать кодировочной.
Первая широко используемая кодировочная таблица была создана в США и называлась ASCII, что в переводе означало American standard code for information interchange. Как вы видите, в таблице присутствуют не только латинские буквы, но и цифры, и даже действия. Каждому символу отводится 7 бит, а значит, всего было закодировано 128 символов.
Но так как этого количества было недостаточно, стали создаваться другие таблицы, в которых можно было закодировать и другие символы. Например, таблица Windows-1251, которая, по сути, являлась изменением таблицы ASCII, в которую добавили буквы кириллицы. Таких таблиц было создано множество: MS-DOS, КОИ-8, ISO, Mac и другие:
Проблема использования таких различных таблиц приводила к тому, что текст, написанный на одном компьютере, мог некорректно читаться на другом. Например:
Поэтому была разработана международная таблица кодировки Unicode, включающая в себя как символы английского, русского, немецкого, арабского и других языков. На каждый символ в такой таблице отводится 16 бит, то есть она позволяет кодировать 65536 символов. Однако использование такой таблицы сильно «утяжеляет» текст. Поэтому существуют различные алгоритмы неравномерной кодировки текста, например, алгоритм Хаффмана.
АЛГОРИТМ ХАФФМАНА
Идея алгоритма Хаффмана основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код.
Пусть нам дано сообщение aaabcbeeffaabfffedbac.
Чтобы узнать наиболее выгодный префиксный код для такого сообщения, надо узнать частоту появления каждого символа в сообщении.
Шаг 1.
Подсчитайте и внесите в таблицу частоту появления каждого символа в сообщении:
У вас должно получиться:
Шаг 2.
Расположите буквы в порядке возрастания их частоты.
Шаг 3.
Теперь возьмем два символа с наименьшей чистотой и представим их листьями в дереве, частота которого будет равна сумме частот этих листьев.
Символы d и c превращаются в ветку дерева:
Шаг 4.
Проделываем эти шаги до тех пор, пока не получится дерево, содержащее все символы.
Итак, сортируем таблицу:
Шаг 5.
Объединяем символ e и символ cd в ветку дерева:
d
C
Шаг 6.
Сортируем:
Шаг 7.
Шаг 8.
Сортируем:
Шаг 9.
Шаг 10.
Сортируем:
Шаг 11.
Шаг 12.
Получился префиксный код. Теперь осталось расставить 1 и 0. Пусть каждая правая ветвь обозначает 1, а левая — 0.
Шаг 13.
Составляем код буквы, идя по ветке дерева от буквы к основанию дерева.
Тогда код для каждой буквы будет:
Задание №1
Закодируйте ASCII кодом слово MOSCOW.
Решение:
Составим таблицу и поместим туда слово MOSCOW. Используя таблицу ASCII кодов, закодируем все буквы слова:
|
M |
O |
S |
C |
O |
W |
|
1001101 |
1001111 |
1010011 |
1000011 |
1001111 |
1110111 |
ОТВЕТ: 100110110011111010011100001110011111110111
Задание №2
Используя табличный код Windows1251, закодируйте слово КОМПЬЮТЕР.
Решение:
|
К |
О |
М |
П |
Ь |
Ю |
Т |
Е |
Р |
|
234 |
206 |
204 |
239 |
252 |
254 |
242 |
197 |
208 |
Ответ: 234206204239252254242197208
Задание №3
Используя алгоритма Хаффмана, закодируйте сообщение: Россия
Решение:
Давайте все левые ветви обозначим «1», а правые – «0»
Таким образом: С — 0, Р — 101, О — 100, И — 111, Я — 110
ОТВЕТ: 10110000111110
Windows-1251 (cp1251) — это стандартная 8-битная кодировка, разработанная компанией Microsoft. Она содержит практически все символы, которые Вы можете встретить на стандартной русской клавиатуре. Также 1251 имеет символы для таких языков, как белорусский, украинский, болгарский и сербский.
|
DEC |
HEX |
СИМВ |
DEC |
HEX |
СИМВ |
DEC |
HEX |
СИМВ |
|
000 |
00 |
NOP |
086 |
56 |
V |
171 |
AB |
« |
|
001 |
01 |
SOH |
087 |
57 |
W |
172 |
AC |
¬ |
|
002 |
02 |
STX |
088 |
58 |
X |
173 |
AD |
|
|
003 |
03 |
ETX |
089 |
59 |
Y |
174 |
AE |
® |
|
004 |
04 |
EOT |
090 |
5A |
Z |
175 |
AF |
Ї |
|
005 |
05 |
ENQ |
091 |
5B |
[ |
176 |
B0 |
° |
|
006 |
06 |
ACK |
092 |
5C |
\ |
177 |
B1 |
± |
|
007 |
07 |
BEL |
093 |
5D |
] |
178 |
B2 |
І |
|
008 |
08 |
BS |
094 |
5E |
^ |
179 |
B3 |
і |
|
009 |
09 |
Табуляция |
095 |
5F |
_ |
180 |
B4 |
ґ |
|
010 |
0A |
LF |
096 |
60 |
` |
181 |
B5 |
µ |
|
011 |
0B |
VT |
097 |
61 |
a |
182 |
B6 |
¶ |
|
012 |
0C |
FF |
098 |
62 |
b |
183 |
B7 |
· |
|
013 |
0D |
CR |
099 |
63 |
c |
184 |
B8 |
Ё |
|
014 |
0E |
SO |
100 |
64 |
d |
185 |
B9 |
№ |
|
015 |
0F |
SI |
101 |
65 |
e |
186 |
BA |
Є |
|
016 |
10 |
DLE |
102 |
66 |
f |
187 |
BB |
» |
|
017 |
11 |
DC1 |
103 |
67 |
g |
188 |
BC |
ј |
|
018 |
12 |
DC2 |
104 |
68 |
h |
189 |
BD |
Ѕ |
|
019 |
13 |
DC3 |
105 |
69 |
i |
190 |
BE |
Ѕ |
|
020 |
14 |
DC4 |
106 |
6A |
j |
191 |
BF |
Ї |
|
021 |
15 |
NAK |
107 |
6B |
k |
192 |
C0 |
А |
|
022 |
16 |
SYN |
108 |
6C |
l |
193 |
C1 |
Б |
|
023 |
17 |
ETB |
109 |
6D |
m |
194 |
C2 |
В |
|
024 |
18 |
CAN |
110 |
6E |
n |
195 |
C3 |
Г |
|
025 |
19 |
EM |
111 |
6F |
o |
196 |
C4 |
Д |
|
026 |
1A |
SUB |
112 |
70 |
p |
197 |
C5 |
Е |
|
027 |
1B |
ESC |
113 |
71 |
q |
198 |
C6 |
Ж |
|
028 |
1C |
FS |
114 |
72 |
r |
199 |
C7 |
З |
|
029 |
1D |
GS |
115 |
73 |
s |
200 |
C8 |
И |
|
030 |
1E |
RS |
116 |
74 |
t |
201 |
C9 |
Й |
|
031 |
1F |
US |
117 |
75 |
u |
202 |
CA |
К |
|
032 |
20 |
Пробел |
118 |
76 |
v |
203 |
CB |
Л |
|
033 |
21 |
! |
119 |
77 |
w |
204 |
CC |
М |
|
034 |
22 |
« |
120 |
78 |
x |
205 |
CD |
Н |
|
035 |
23 |
# |
121 |
79 |
y |
206 |
CE |
О |
|
036 |
24 |
$ |
122 |
7A |
z |
207 |
CF |
П |
|
037 |
25 |
% |
123 |
7B |
{ |
208 |
D0 |
Р |
|
038 |
26 |
& |
124 |
7C |
| |
209 |
D1 |
С |
|
039 |
27 |
‘ |
125 |
7D |
} |
210 |
D2 |
Т |
|
040 |
28 |
( |
126 |
7E |
~ |
211 |
D3 |
У |
|
041 |
29 |
) |
127 |
7F |
|
212 |
D4 |
Ф |
|
042 |
2A |
* |
128 |
80 |
Ђ |
213 |
D5 |
Х |
|
043 |
2B |
+ |
129 |
81 |
Ѓ |
214 |
D6 |
Ц |
|
044 |
2C |
, |
130 |
82 |
‚ |
215 |
D7 |
Ч |
|
045 |
2D |
— |
131 |
83 |
ѓ |
216 |
D8 |
Ш |
|
046 |
2E |
. |
132 |
84 |
„ |
217 |
D9 |
Щ |
|
047 |
2F |
/ |
133 |
85 |
… |
218 |
DA |
Ъ |
|
048 |
30 |
0 |
134 |
86 |
† |
219 |
DB |
Ы |
|
049 |
31 |
1 |
135 |
87 |
‡ |
220 |
DC |
Ь |
|
050 |
32 |
2 |
136 |
88 |
€ |
221 |
DD |
Э |
|
051 |
33 |
3 |
137 |
89 |
‰ |
222 |
DE |
Ю |
|
052 |
34 |
4 |
138 |
8A |
Љ |
223 |
DF |
Я |
|
053 |
35 |
5 |
139 |
8B |
‹ |
224 |
E0 |
а |
|
054 |
36 |
6 |
140 |
8C |
Њ |
225 |
E1 |
б |
|
055 |
37 |
7 |
141 |
8D |
Ќ |
226 |
E2 |
в |
|
056 |
38 |
8 |
142 |
8E |
Ћ |
227 |
E3 |
г |
|
057 |
39 |
9 |
143 |
8F |
Џ |
228 |
E4 |
д |
|
058 |
3A |
: |
144 |
90 |
Ђ |
229 |
E5 |
е |
|
059 |
3B |
; |
145 |
91 |
‘ |
230 |
E6 |
ж |
|
060 |
3C |
< |
146 |
92 |
’ |
231 |
E7 |
з |
|
061 |
3D |
= |
147 |
93 |
“ |
232 |
E8 |
и |
|
062 |
3E |
> |
148 |
94 |
” |
233 |
E9 |
й |
|
063 |
3F |
? |
149 |
95 |
• |
234 |
EA |
к |
|
064 |
40 |
@ |
150 |
96 |
– |
235 |
EB |
л |
|
065 |
41 |
A |
151 |
97 |
— |
236 |
EC |
м |
|
066 |
42 |
B |
152 |
98 |
237 |
ED |
н |
|
|
067 |
43 |
C |
153 |
99 |
™ |
238 |
EE |
о |
|
068 |
44 |
D |
154 |
9A |
љ |
239 |
EF |
п |
|
069 |
45 |
E |
155 |
9B |
› |
240 |
F0 |
р |
|
070 |
46 |
F |
156 |
9C |
њ |
241 |
F1 |
с |
|
071 |
47 |
G |
157 |
9D |
ќ |
242 |
F2 |
т |
|
072 |
48 |
H |
158 |
9E |
ћ |
243 |
F3 |
у |
|
073 |
49 |
I |
159 |
9F |
џ |
244 |
F4 |
ф |
|
074 |
4A |
J |
160 |
A0 |
245 |
F5 |
х |
|
|
075 |
4B |
K |
161 |
A1 |
Ў |
246 |
F6 |
ц |
|
076 |
4C |
L |
162 |
A2 |
ў |
247 |
F7 |
ч |
|
077 |
4D |
M |
163 |
A3 |
Ј |
248 |
F8 |
ш |
|
078 |
4E |
N |
164 |
A4 |
¤ |
249 |
F9 |
щ |
|
079 |
4F |
O |
165 |
A5 |
Ґ |
250 |
FA |
ъ |
|
080 |
50 |
P |
166 |
A6 |
¦ |
251 |
FB |
ы |
|
081 |
51 |
Q |
167 |
A7 |
§ |
252 |
FC |
ь |
|
082 |
52 |
R |
168 |
A8 |
Ё |
253 |
FD |
э |
|
083 |
53 |
S |
169 |
A9 |
© |
254 |
FE |
ю |
|
084 |
54 |
T |
170 |
AA |
Є |
255 |
FF |
я |
|
085 |
55 |
U |
Таблица ASCII (American standard code for information interchange) является мировым стандартом для кодирования букв английского алфавита, популярных спец символов (! $ # % & и т.д.) и некоторых непечатных символов (например, возврат каретки 0x0D и перенос строки 0х0А).
Таблица создавалась те времена, когда возникла необходимость связать символы и числа. А такое соответствие необходимо было для того что бы с помощью чисел можно было передать текстовое сообщение между разными устройствами с цифровой связью.
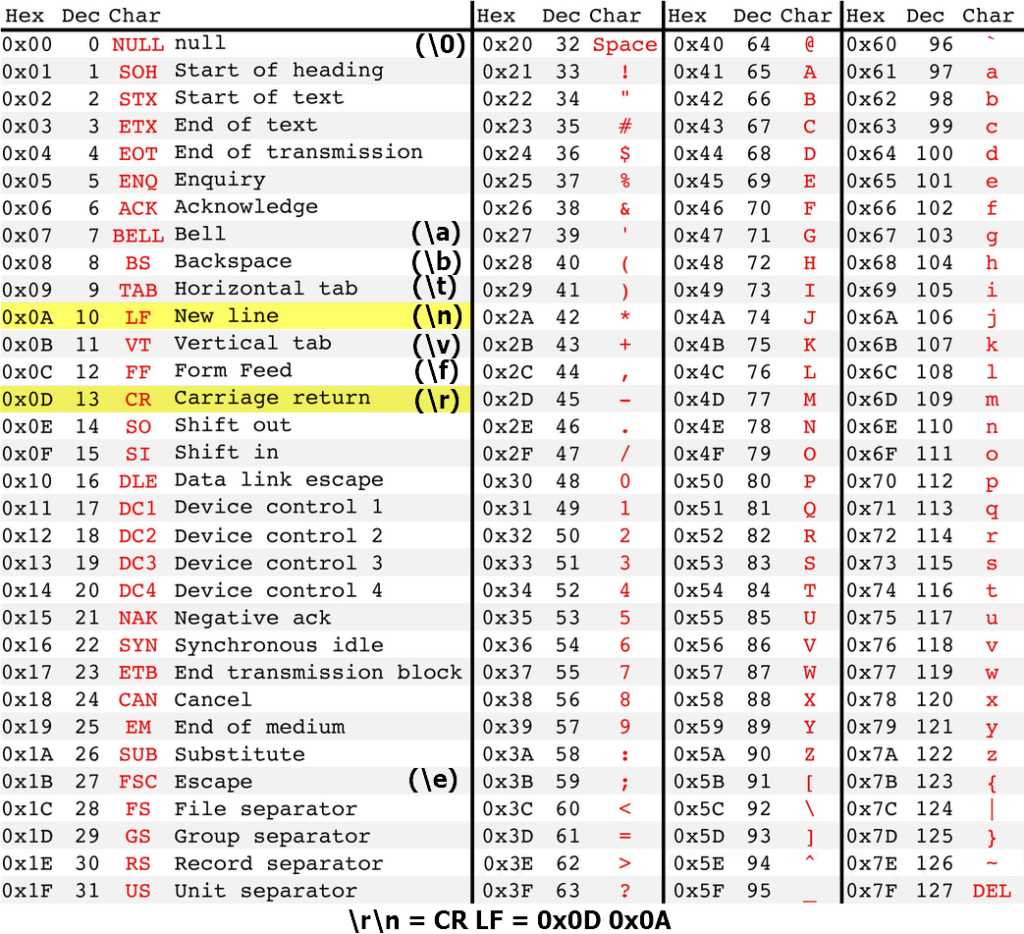
Таблица CP1251 (windows-1251)
Эта кодировочная таблица может называться или CP1251 или Windows-1251 Это стандарт кодирования кириллических символов в операционных системах windows с русскоязычным интерфейсом.
Первая часть этой таблицы (до байта 0x7F) повторяет таблицу ASCII, а вторая часть (от 0x80 до 0xFF) кодирует кириллические символы в алфавитном порядке.

Таблица IS0-8859-5
Эта кодировка применяется в дисплеях Nextion для кодирования кириллических символов.
Стоит обратить внимание, что в данной таблице кириллические символы расположены в алфавитном порядке и сдвинуты ровно на 16 байт по сравнению с кодировочной таблицей windows-1251.

Кодировка UTF-8
(Unicode Transformation Format)
Очень распространенный формат кодирования символов, позволяющий кодировать символы переменным количеством байт.
Например, если для кодирования номера символа требуется 21 бит, то используется 4 байта для кодировки. Если для кодирования достаточно 11 бит, то используют 2 байта. А если номер символа может быть закодирован 7 битами, то используется один байт.

Все ASCII символы в кодировке UTF8 закодированы без изменений, то есть 1 байтом, как в стандартной таблице ASCII.
А вот остальные символы закодированы количеством байт от 2 до 4.
Кириллические символы закодированы двумя байтами.